A red-black tree is a kind of self-balancing binary search tree. Each node stores an extra bit, which we will call the color, red or black. The color ensures that the tree remains approximately balanced during insertions and deletions. When the tree is modified, the new tree is rearranged and repainted to restore the coloring properties that constrain how unbalanced the tree can become in the worst case.
The purpose of a red-black tree is to stay balanced which ensures that its common operations, like lookup and delete, never degrade to worse than O(n*log(n)).
What is a balanced binary tree? 🔗
Since the reason colors are added to a binary tree is to ensure that it remains balanced, we need to understand how and why a binary tree is balanced. To put it simply, a balanced tree’s branches differ in height by no more than 1.
The following tree is balanced because between its two branches one has a height of 2, and the other 3, meaning they differ by no more than 1.
A
/ \
B C
/
D
The next tree is unbalanced because it’s branches differ in height by more than 1. C’s right side has a height of 2 while its left side has a height of 4).
A
/ \
B C
/ /
D E
/
G
Why do we want balanced trees? 🔗
Balanced binary search trees ensure speed. The speed of an operation in a binary tree depends on the height of the tree. If the tree is balanced, then the height is only the log of the number of nodes, which means the tree will work as fast as possible. However, if the tree is unbalanced, for example with one really long branch, then the height because the total number of nodes rather than the log.
A
/
B
/
C
/
D
Properties of a red-black tree 🔗
In addition to all the properties of a Binary Search Tree, a red-black tree must have the following:
- Each node is either red or black
- The root is black. This rule is sometimes omitted. Since the root can always be changed from red to black, but not necessarily vice versa, this rule has little effect on analysis.
- All
nilleaf nodes are black. - If a node is red, then both its children are black.
- All paths from a single node go through the same number of black nodes to reach any of its descendant
nilnodes.
Implementing a Red-Black Tree in Python 🔗
Step 1 – RBNode Class 🔗
Our implementation will use a Tree class and a Node class. The Node will be fairly simple, it’s just a constructor.
class RBNode:
def __init__(self, val):
self.red = False
self.parent = None
self.val = val
self.left = None
self.right = None
Step 2 – RBTree Class 🔗
Next let’s create a tree class with a constructor.
class RBTree:
def __init__(self):
self.nil = RBNode(0)
self.nil.red = False
self.nil.left = None
self.nil.right = None
self.root = self.nil
Step 3 - Insert method 🔗
def insert(self, val):
# Ordinary Binary Search Insertion
new_node = RBNode(val)
new_node.parent = None
new_node.left = self.nil
new_node.right = self.nil
new_node.red = True # new node must be red
parent = None
current = self.root
while current != self.nil:
parent = current
if new_node.val < current.val:
current = current.left
elif new_node.val > current.val:
current = current.right
else:
return
# Set the parent and insert the new node
new_node.parent = parent
if parent == None:
self.root = new_node
elif new_node.val < parent.val:
parent.left = new_node
else:
parent.right = new_node
# Fix the tree
self.fix_insert(new_node)
The insert method will look a lot like a traditional binary tree insert method. The biggest difference is that after doing an insert, we’ll call a special fix_insert method. For now just call it, we’ll implement it in just a moment.
Step 4 - Rotate left 🔗
We’ll need some rotation methods in our “fix” step that’s coming up. Let’s code those now.
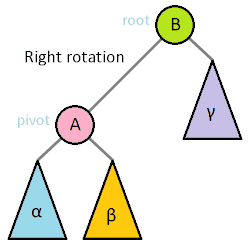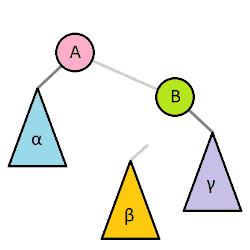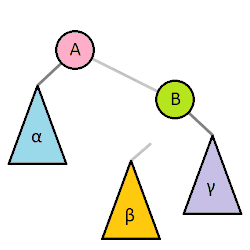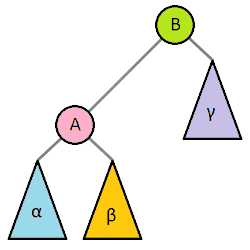
# rotate left at node x
def rotate_left(self, x):
y = x.right
x.right = y.left
if y.left != self.nil:
y.left.parent = x
y.parent = x.parent
if x.parent == None:
self.root = y
elif x == x.parent.left:
x.parent.left = y
else:
x.parent.right = y
y.left = x
x.parent = y
Step 5 - Rotate right 🔗
# rotate right at node x
def rotate_right(self, x):
y = x.left
x.left = y.right
if y.right != self.nil:
y.right.parent = x
y.parent = x.parent
if x.parent == None:
self.root = y
elif x == x.parent.right:
x.parent.right = y
else:
x.parent.left = y
y.right = x
x.parent = y
Step 6 - Fix insert 🔗
The real bread and butter is in this step, it’s what makes a red-black tree balanced.
def fix_insert(self, new_node):
while new_node != self.root and new_node.parent.red:
if new_node.parent == new_node.parent.parent.right:
u = new_node.parent.parent.left # uncle
if u.red:
u.red = False
new_node.parent.red = False
new_node.parent.parent.red = True
new_node = new_node.parent.parent
else:
if new_node == new_node.parent.left:
new_node = new_node.parent
self.rotate_right(new_node)
new_node.parent.red = False
new_node.parent.parent.red = True
self.rotate_left(new_node.parent.parent)
else:
u = new_node.parent.parent.right # uncle
if u.red:
u.red = False
new_node.parent.red = False
new_node.parent.parent.red = True
new_node = new_node.parent.parent
else:
if new_node == new_node.parent.right:
new_node = new_node.parent
self.rotate_left(new_node)
new_node.parent.red = False
new_node.parent.parent.red = True
self.rotate_right(new_node.parent.parent)
self.root.red = False
Full Example of Red-Black Tree in Code 🔗
import random
class RBNode:
def __init__(self, val):
self.red = False
self.parent = None
self.val = val
self.left = None
self.right = None
class RBTree:
def __init__(self):
self.nil = RBNode(0)
self.nil.red = False
self.nil.left = None
self.nil.right = None
self.root = self.nil
def insert(self, val):
# Ordinary Binary Search Insertion
new_node = RBNode(val)
new_node.parent = None
new_node.left = self.nil
new_node.right = self.nil
new_node.red = True # new node must be red
parent = None
current = self.root
while current != self.nil:
parent = current
if new_node.val < current.val:
current = current.left
elif new_node.val > current.val:
current = current.right
else:
return
# Set the parent and insert the new node
new_node.parent = parent
if parent == None:
self.root = new_node
elif new_node.val < parent.val:
parent.left = new_node
else:
parent.right = new_node
# Fix the tree
self.fix_insert(new_node)
def fix_insert(self, new_node):
while new_node != self.root and new_node.parent.red:
if new_node.parent == new_node.parent.parent.right:
u = new_node.parent.parent.left # uncle
if u.red:
u.red = False
new_node.parent.red = False
new_node.parent.parent.red = True
new_node = new_node.parent.parent
else:
if new_node == new_node.parent.left:
new_node = new_node.parent
self.rotate_right(new_node)
new_node.parent.red = False
new_node.parent.parent.red = True
self.rotate_left(new_node.parent.parent)
else:
u = new_node.parent.parent.right # uncle
if u.red:
u.red = False
new_node.parent.red = False
new_node.parent.parent.red = True
new_node = new_node.parent.parent
else:
if new_node == new_node.parent.right:
new_node = new_node.parent
self.rotate_left(new_node)
new_node.parent.red = False
new_node.parent.parent.red = True
self.rotate_right(new_node.parent.parent)
self.root.red = False
def exists(self, val):
curr = self.root
while curr != self.nil and val != curr.val:
if val < curr.val:
curr = curr.left
else:
curr = curr.right
return curr
# rotate left at node x
def rotate_left(self, x):
y = x.right
x.right = y.left
if y.left != self.nil:
y.left.parent = x
y.parent = x.parent
if x.parent == None:
self.root = y
elif x == x.parent.left:
x.parent.left = y
else:
x.parent.right = y
y.left = x
x.parent = y
# rotate right at node x
def rotate_right(self, x):
y = x.left
x.left = y.right
if y.right != self.nil:
y.right.parent = x
y.parent = x.parent
if x.parent == None:
self.root = y
elif x == x.parent.right:
x.parent.right = y
else:
x.parent.left = y
y.right = x
x.parent = y
def __repr__(self):
lines = []
print_tree(self.root, lines)
return '\n'.join(lines)
def print_tree(node, lines, level=0):
if node.val != 0:
print_tree(node.left, lines, level + 1)
lines.append('-' * 4 * level + '> ' +
str(node.val) + ' ' + ('r' if node.red else 'b'))
print_tree(node.right, lines, level + 1)
def get_nums(num):
random.seed(1)
nums = []
for _ in range(num):
nums.append(random.randint(1, num-1))
return nums
def main():
tree = RBTree()
for x in range(1, 51):
tree.insert(x)
print(tree)
main()




