What is a binary search tree? 🔗
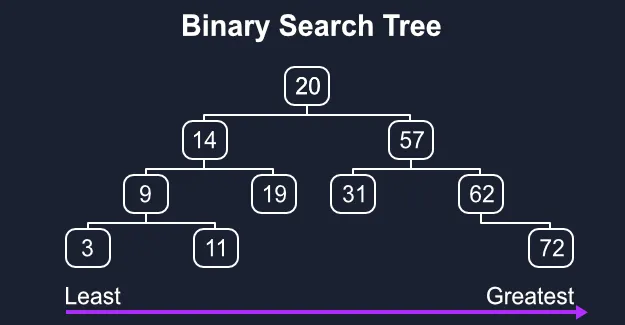
A binary search tree, or BST for short, is a tree where each node is a value greater than all of its left child nodes and less than all of its right child nodes. Read on for an implementation of a binary search tree in Python from scratch!
Subscribe to my YouTube channel if this video was helpful!
Also, if you’re interested in really learning this stuff, you should check out three of my courses:
Why would I use a binary search tree? 🔗
Binary trees are useful for storing data in an organized manner so that it can be quickly retrieved, inserted, updated, and deleted. This arrangement of nodes allows each comparison to skip about half of the rest of the tree, so each operation as a whole is lightning fast.
To be precise, binary search trees provide an average Big-O complexity of O(log(n)) for search, insert, update, and delete operations. log(n) is much faster than the linear O(n) time required to find elements in an unsorted array. Many popular production databases such as PostgreSQL and MySQL use binary trees under the hood to speed up CRUD operations.
Pros of a BST 🔗
- When balanced, a BST provides lightning-fast
O(log(n))insertions, deletions, and lookups. - Binary search trees are simple to implement. An ordinary BST, unlike a balanced red-black tree, requires very little code to get running.
Cons of a BST 🔗
- Slow for a brute-force search. If you need to iterate over each node, you might have more success with an array.
- When the tree becomes unbalanced, all fast
O(log(n))operations quickly degrade toO(n). - Since pointers to whole objects are typically involved, a BST can require quite a bit more memory than an array, although this depends on the implementation.
Implementing a B-tree in Python 🔗
Step 1 - BSTNode Class 🔗
Our implementation won’t use a Tree class, but instead just a Node class. Binary trees are really just a pointer to a root node that in turn connects to each child node, so we’ll run with that idea.
First, we create a constructor:
class BSTNode:
def __init__(self, val=None):
self.left = None
self.right = None
self.val = val
We’ll allow a value, which will also act as the key, to be provided. If one isn’t provided we’ll just set it to None. We’ll also initialize both children of the new node to None.
Step 2 - Insert 🔗

We need a way to insert new data into the tree. Inserting a new node should append it as a leaf node in the proper spot.
10 10
/ \ Insert 5 / \
2 60 ---------> 2 60
/ \ / \
1 3 1 3
\
5
The insert method is as follows:
def insert(self, val):
if not self.val:
self.val = val
return
if self.val == val:
return
if val < self.val:
if self.left:
self.left.insert(val)
return
self.left = BSTNode(val)
return
if self.right:
self.right.insert(val)
return
self.right = BSTNode(val)
If the node doesn’t yet have a value, we can just set the given value and return. If we ever try to insert a value that also exists, we can also simply return as this can be considered a “no-op”. If the given value is less than our node’s value and we already have a left child then we recursively call insert on our left child. If we don’t have a left child yet then we just make the given value our new left child. We can do the same (but inverted) for our right side.
Step 3 - Get Min and Get Max 🔗
def get_min(self):
current = self
while current.left is not None:
current = current.left
return current.val
def get_max(self):
current = self
while current.right is not None:
current = current.right
return current.val
getMin and getMax are useful helper functions, and they’re easy to write! They are simple recursive functions that traverse the edges of the tree to find the smallest or largest values stored therein.
Step 4 - Delete 🔗
def delete(self, val):
if self == None:
return self
if val < self.val:
self.left = self.left.delete(val)
return self
if val > self.val:
self.right = self.right.delete(val)
return self
if self.right == None:
return self.left
if self.left == None:
return self.right
min_larger_node = self.right
while min_larger_node.left:
min_larger_node = min_larger_node.left
self.val = min_larger_node.val
self.right = self.right.delete(min_larger_node.val)
return self
The delete operation is one of the more complex ones. It is a recursive function as well, but it also returns the new state of the given node after performing the delete operation. This allows a parent whose child has been deleted to properly set it’s left or right data member to None.
Step 5 - Exists 🔗
The exists function is another simple recursive function that returns True or False depending on whether a given value already exists in the tree.
def exists(self, val):
if val == self.val:
return True
if val < self.val:
if self.left == None:
return False
return self.left.exists(val)
if self.right == None:
return False
return self.right.exists(val)
Step 6 - Inorder 🔗
It’s useful to be able to print out the tree in a readable format. The inorder method print’s the values in the tree in the order of their keys.
def inorder(self, vals):
if self.left is not None:
self.left.inorder(vals)
if self.val is not None:
vals.append(self.val)
if self.right is not None:
self.right.inorder(vals)
return vals
Step 7 - Preorder 🔗
def preorder(self, vals):
if self.val is not None:
vals.append(self.val)
if self.left is not None:
self.left.preorder(vals)
if self.right is not None:
self.right.preorder(vals)
return vals
Step 8 - Postorder 🔗
def postorder(self, vals):
if self.left is not None:
self.left.postorder(vals)
if self.right is not None:
self.right.postorder(vals)
if self.val is not None:
vals.append(self.val)
return vals
Using the BST 🔗
def main():
nums = [12, 6, 18, 19, 21, 11, 3, 5, 4, 24, 18]
bst = BSTNode()
for num in nums:
bst.insert(num)
print("preorder:")
print(bst.preorder([]))
print("#")
print("postorder:")
print(bst.postorder([]))
print("#")
print("inorder:")
print(bst.inorder([]))
print("#")
nums = [2, 6, 20]
print("deleting " + str(nums))
for num in nums:
bst.delete(num)
print("#")
print("4 exists:")
print(bst.exists(4))
print("2 exists:")
print(bst.exists(2))
print("12 exists:")
print(bst.exists(12))
print("18 exists:")
print(bst.exists(18))
Full Binary Search Tree in Python 🔗
class BSTNode:
def __init__(self, val=None):
self.left = None
self.right = None
self.val = val
def insert(self, val):
if not self.val:
self.val = val
return
if self.val == val:
return
if val < self.val:
if self.left:
self.left.insert(val)
return
self.left = BSTNode(val)
return
if self.right:
self.right.insert(val)
return
self.right = BSTNode(val)
def get_min(self):
current = self
while current.left is not None:
current = current.left
return current.val
def get_max(self):
current = self
while current.right is not None:
current = current.right
return current.val
def delete(self, val):
if self == None:
return self
if self.right == None:
return self.left
if self.left == None:
return self.right
if val < self.val:
if self.left:
self.left = self.left.delete(val)
return self
if val > self.val:
if self.right:
self.right = self.right.delete(val)
return self
min_larger_node = self.right
while min_larger_node.left:
min_larger_node = min_larger_node.left
self.val = min_larger_node.val
self.right = self.right.delete(min_larger_node.val)
return self
def exists(self, val):
if val == self.val:
return True
if val < self.val:
if self.left == None:
return False
return self.left.exists(val)
if self.right == None:
return False
return self.right.exists(val)
def preorder(self, vals):
if self.val is not None:
vals.append(self.val)
if self.left is not None:
self.left.preorder(vals)
if self.right is not None:
self.right.preorder(vals)
return vals
def inorder(self, vals):
if self.left is not None:
self.left.inorder(vals)
if self.val is not None:
vals.append(self.val)
if self.right is not None:
self.right.inorder(vals)
return vals
def postorder(self, vals):
if self.left is not None:
self.left.postorder(vals)
if self.right is not None:
self.right.postorder(vals)
if self.val is not None:
vals.append(self.val)
return vals
Where would you use a binary search tree in real life? 🔗
There are many applications of binary search trees in real life, and one of the most common use cases is in storing indexes and keys in a database.
For example, in MySQL or PostgreSQL when you create a primary key column, what you’re really doing is creating a binary tree where the keys are the values of the column, and those nodes point to database rows. This lets the application easily search database rows by providing a key. For example, getting a user record by the email primary key.
There are many applications of binary search trees in real life, and one of the most common use cases is storing indexes and keys in a database.
For example, when you create a primary key column in MySQL or PostgreSQL, you create a binary tree where the keys are the values of the column and the nodes point to database rows. This allows the application to easily search for database rows by specifying a key, for example, to find a user record using the email primary key.
Other common uses include:
- Pathfinding algorithms in video games (A*) use BSTs
- File compression using a Huffman encoding scheme uses a binary search tree
- Rendering calculations - Doom (1993) was famously the first game to use a BST
- Compilers for low-level coding languages parse syntax using a BST
- Almost every database in existence uses BSTs for key lookups
What’s the difference between a Binary Tree and a Linked List? 🔗
While binary trees and linked lists both use pointers to keep track of nodes, binary trees are more efficient for searching. In fact, linked lists are O(n) when used to search for a specific element - that’s pretty bad! Linked lists excel at removing and inserting elements quickly in the middle of the list.




