You’ve probably visited a site and attempted to sign-up only to be met with errors such as:
- Password needs a capital letter
- Password needs a special character
- Password needs to be at least 8 characters
I just released a package in Go that solves this problem. Check it out and give it a star here: go-password-validator. If you want to understand how it works, and how to properly validate user passwords, read on.
Not only are the rules above quite annoying, but they can also be a security flaw in the system. Take for example a strong passphrase: super worm eaten human trike. That passphrase has plenty of entropy (randomness) but it wouldn’t pass the first two validation steps given above. XKCD puts this best:
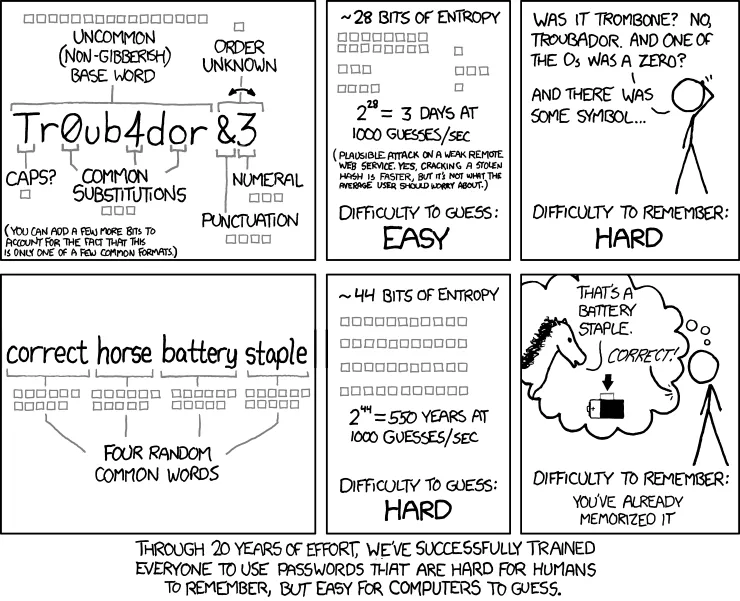
The Problem - Allow Users to Use Any Password Format as Long as It Has Enough Entropy 🔗
We don’t care if a password only has lowercase letters if it’s long. All that matters is the entropy. Entropy in this context refers to the number of brute-force guesses it would take to guess a password, and we measure it in bits (the exponent in 2^n). Refer to the following chart to see how various entropy levels contribute to the time it takes to brute force a password.
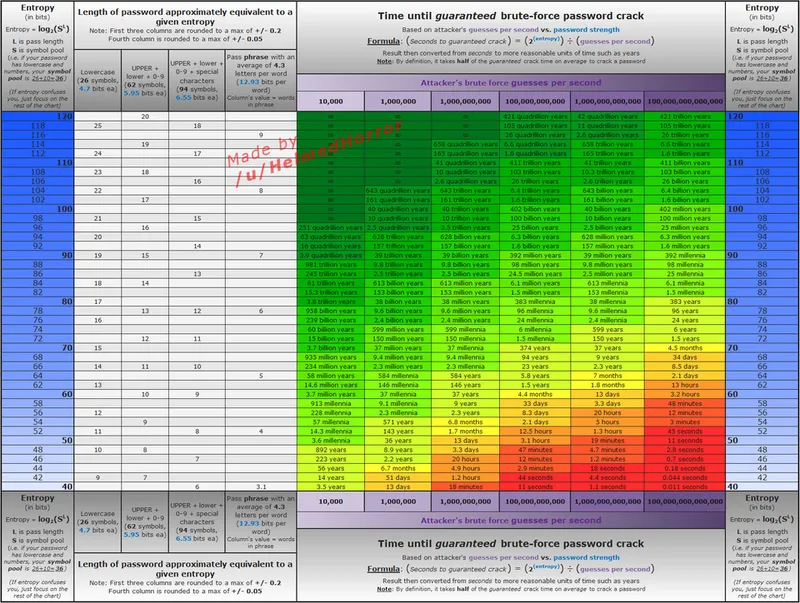
How To Determine Entropy Given a Password 🔗
The way go-password-validator works is my favorite (obviously, I wrote it), but there is certainly room for improvement. Let’s take a look at the process. From its Readme:
First, we determine the “base” number. The base is a sum of the different “character sets” found in the password.
The current character sets include:
- 26 lowercase letters
- 26 uppercase
- 10 digits
- 32 special characters -
!"#$%&'()*+,-./:;<=>?@[\]^_{|}~
Using at least one character from each set your base number will be 94: 26+26+10+32 = 94
Every unique character that doesn’t match one of those sets will add 1 to the base.
If you only use, for example, lowercase letters and numbers, your base will be 36: 26+10 = 36.
After we have calculated a base, the total number of brute-force-guesses is found using the following formulae: base^length
A password using base 26 with 7 characters would require 26^7, or 8031810176 guesses.
Once we know the number of guesses it would take, we can calculate the actual entropy in bits using log2(guesses)




