To “Brute Force” something (when talking about computers) means to systematically try every possible combination until you find the right answer.
Brute force attackers guess passwords, passphrases, and private keys in an attempt to eventually get the right answer and crack the security of a system. They systematically guess every combination. For example, if they were guessing telephone numbers in the US, they would start with 000-0000 and end with 999-9999:
(000) 000-0000
(000) 000-0001
(000) 000-0002
(000) 000-0003
...
(999) 999-9996
(999) 999-9997
(999) 999-9998
(999) 999-9999
The question is, how do they know when they have the right key? Well, it depends on the system.
Let’s answer the question three times, one for three different common systems.
Cipher Text With Authentication 🔗
In this case, let’s assume we have direct access to an encrypted hard drive (like that of a MacBook) that has been ciphered using AES-256-GCM. Because we have access to the raw encrypted data, we can’t be locked out for too many failed attempts. 😈
Since we are free to guess as hard and as fast as we can, all we need to know is when to stop deciphering. This is easy if the encryption was done using an authentication tag as required by GCM mode. When we get the correct password, the authentication tag will check out.
Web Application 🔗
Brute forcing your way through the front door of a web application will prove difficult if not impossible. The cryptosystem lives on a server you don’t have control over. Due to this, they can lock you out after a number of failed guesses.
However, if the server doesn’t have these kinds of protections in place, then it is easy to tell when you have the right password because you will likely be given an HTTP 200 response OK, and perhaps some form of login token.
Public-Private Key Encryption 🔗
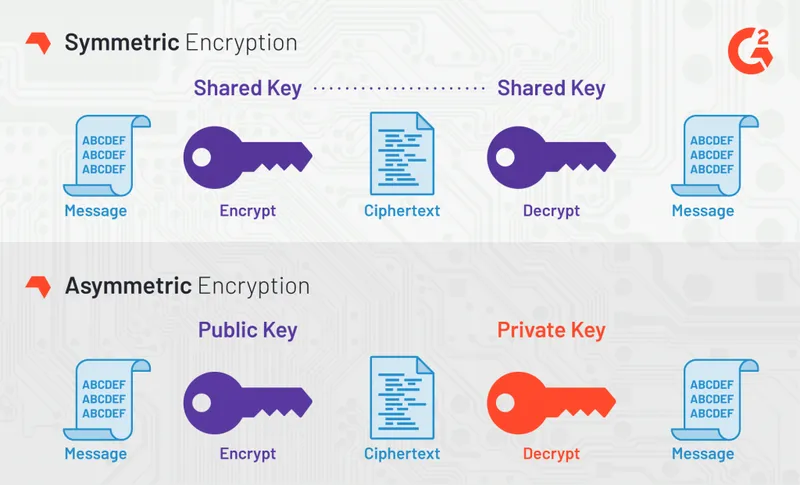
Symmetric Cipher vs Asymmetric Public Key Encryption
We can encrypt any message using the public key that we have, and we can decrypt using the private key if we can find it. Then, we can man-in-the-middle attack other users and decrypt their messages that were meant for the server.
Ignoring the fact that it is practically impossible to brute force a 256-bit key, let’s pretend that we have an infinite amount of resources and are able to eventually get the correct answer.
How do we know when we have the right answer?
Well, it depends a bit on the algorithm that was used to create the key pair. If we know the algorithm, then we can generate random private keys and check to see if the public key that we have is a valid match using the known algorithm.
If this isn’t feasible because we don’t have all the algorithm information, then we are likely stuck with encrypting a random string of text with the public key, generating private keys, and trying to decrypt with each private key until the decryption is successful.
Again, this would never work in practicality, the search space is 2^256
Brute-Force Attacks Explained 🔗

A brute-force attack in cryptography is when an attacker guesses many passwords in succession hoping to eventually get one right.
For example, the most naive form of brute force attack would be to try every permutation of characters from length 0 to length n.
a, b, c …
aa, ab, ac, … ba, bb, bc
aaa, aab, aac, … aba, abb, abc… bba, bbb, bbc…
Assuming 26 lowercase letters, 26 uppercase letters, 10 digits, and 10 special characters, it would take 72^10 (~3,740,000,000,000,000,000) guesses just to try all the combinations of exactly length 10. Assuming a modest 200 guesses per second, it would take ~593,592,440 years to crack the password.
So I’m Safe Right? 🔗
Based on the math above, it certainly seems like 10 digit passwords are impervious to brute force attacks. While that may be true of the most naive attacks, there are other things to watch out for.
Instead of the attacker guess every single combination, instead, they may try every word in the English dictionary, with every three-digit combination appended to the end.
- apple001, apple002, apple003…
- baby001, baby002, baby003…
Assuming 50,000 words in the English dictionary, there are only 50,000,000 combinations! Again, assuming 200 guesses per second, it would take ~2.9 days to crack the password… that isn’t very long. It is also trivial for the attacker to throw in special characters for corresponding letters. For example, @pp1e001




